ベン図の問題
ベン図とは
ベン図とは、集合が表す範囲(領域)を図で表現したものです。ベン図は、大きな四角い枠(全体集合)Uの中に、2つの丸い枠(部分集合Aと部分集合B)の一部を重ねて描くのが基本です。
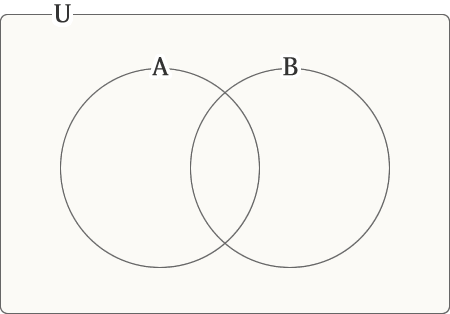
ベン図の基本図
全体集合Uとは、対象となる集合全体を表しています。ベン図の問題は全体集合の中で考えます。そして、部分集合はその全体集合の中の一部です。
例えば、全体集合Uを「1以上10以下の整数」として、部分集合Aを「(1以上10以下の整数の中で)2の倍数」、部分集合Bを「(1以上10以下の整数の中で)3の倍数」のような条件で出題されます。
この場合、全体集合が「1以上10以下の整数」なので、例えば、15は3の倍数ですが、この問題では無視します。
※全体集合や部分集合を単に「集合U」「集合A」「集合B」のように呼ぶこともあります。
ベン図で集合を表現するには
ベン図では、それぞれの集合の領域を斜線や塗りつぶすことで示します。
例えば、次のベン図は部分集合Aを表しています。
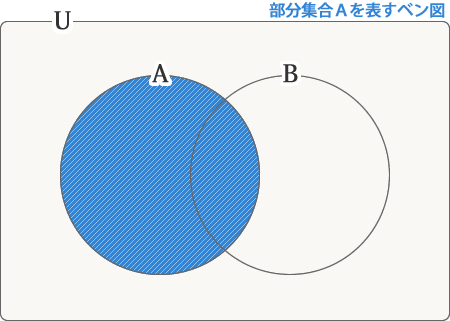
部分集合Aを表すベン図
A∩BとA∪B
∩(キャップ)は2つの集合の共通部分、∪(カップ)は2つの集合を(重ね)合わせた部分です。ベン図に表すと次のようになります。
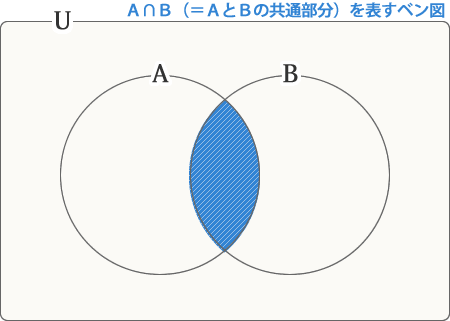
A∩Bを表すベン図
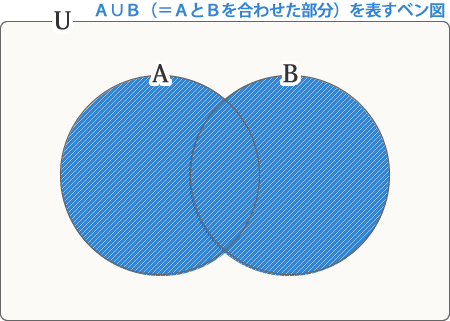
A∪Bを表すベン図
もし、上記の内容が理解できない方は、難しく考えすぎていると思われます。実は、言っていることは超簡単なんです。Aの領域(円形)とBの領域(円形)があって、共通の領域(交わっているところ)が、A∩Bです。そして、2つの領域を合わせた領域がA∪Bです。
∩(キャップ)と∪(カップ)の向きは間違えないように、確実に覚えてくださいね。
と
次のベン図は、全体からAの部分の円形が抜けています(Aの内部が白)。
つまり「Aでない集合」です。これを数学では、 と表現します。
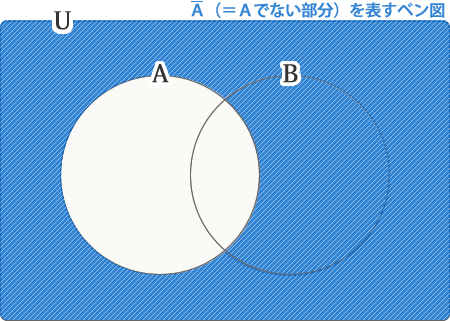
Aバー(Aの否定)を表すベン図
ここでは、ベン図は割愛しますが、も「Bでない集合」なので、ベン図は、全体からBの部分が抜ける図になります(Bの内部が白)。
∩B
次の図は、実際の試験で正解としてよくある図(三日月形のベン図)です。少々難解ですが、このレベルが理解できると、高認の問題もラクに解けるようになるので、ぜひ、頑張ってください。
よく見ると「Aでない部分」と「B」との共通部分(∩キャップ)です。
数学的に表現すると、∩Bです。
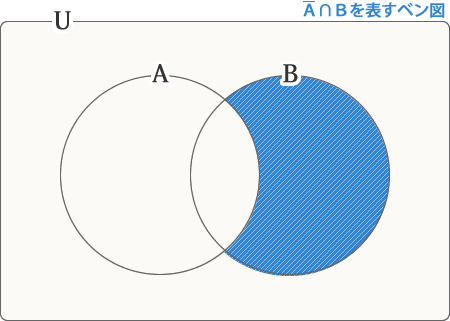
AバーキャップBを表すベン図
よく理解できない人は、下の2つの図を見比べてみてください。あくまでも「Aでない部分」と「B」との共通部分です。共通部分なので、どちらか一方にでも白い領域があれば、そこは共通部分にならないので、必ず除外されます。

Aバー(Aの否定)を表すベン図
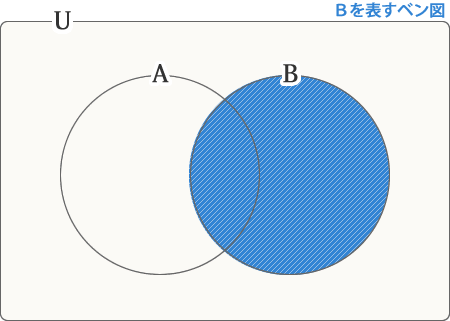
Bを表すベン図
∪B
次の図は比較的簡単です。
「Aでない部分」と「B」とを(単純に)合わせた部分(∪カップ)です。
数学的に表現すると、∪Bとなります。
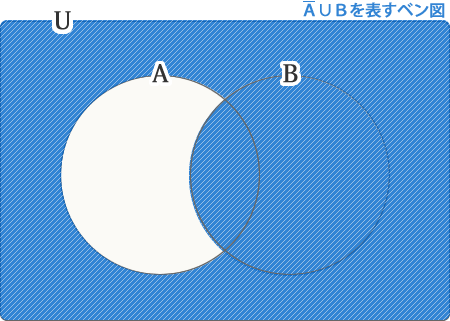
AバーカップBを表すベン図
この∪B(合わせた部分)と、先の∩B(共通部分)とを混同しないように注意してください。ここまで、クリアーできれば、あと残りの2つです。
と∪(←どちらも同じベン図)
次の図は、ある一部分が抜けています。つまり、抜けている白い部分以外の領域を表しています。
抜けているのは、A∩Bの部分(白い部分)です。これ(A∩B)以外の領域を表しているので、になります。
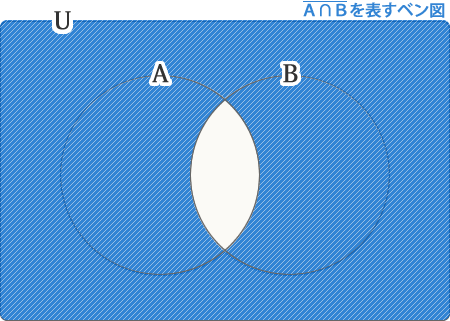
(AキャップB)バーを表すベン図
実はこのベン図には、もう一つの見方があります。それは、との(重ね)合わせた部分ということです。そのため、∪と表すことができます。うまく理解できない方は、次の図をよく見て考えてみてください。
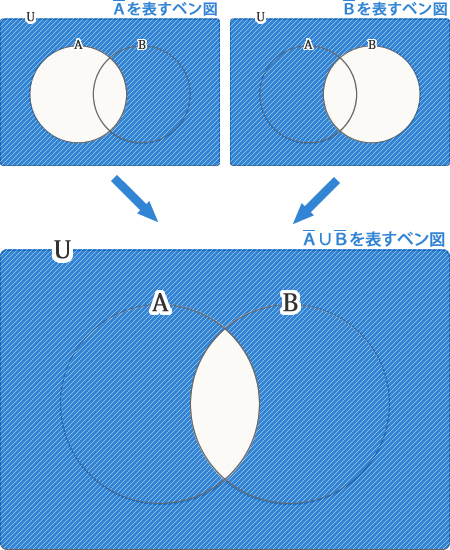
(AバーカップBバー)バーを表すベン図
試験(高卒認定/高認)では、「次のベン図の表す集合はどれか」という問題がよく出題されます。上記のベン図で出題された場合、選択肢の中に、∪または、のどちらかが含まれているので、それを選択すれば正解です。
と∩(←どちらも同じベン図)
次の図で、抜けているのは、A∪Bの部分(白い部分)です。これ以外の領域を表しているので、になります。
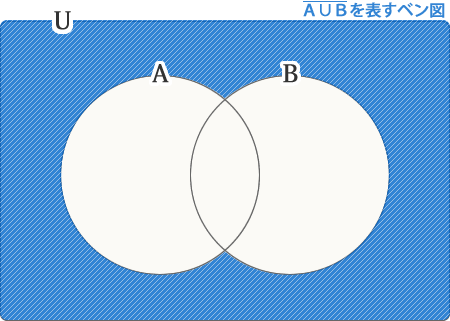
(AキャップB)バーを表すベン図
こちらももう一つの見方があります。ととの共通部分∩です(Aでもなく、Bでもない部分)。次の図でそれを確認してみてください。
共通部分なので、どちらか一方にでも白い部分があったら除外します。
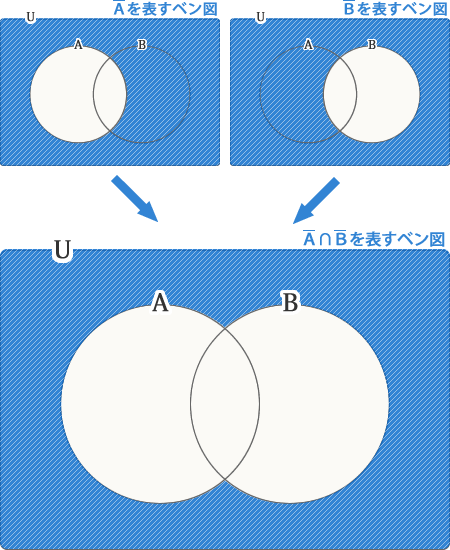
AバーキャップBバーを表すベン図
高認の過去問にチャレンジ・1
次の問題は過去問題です。必要なことは、このページですべて説明してあります。正解だけでなく、正解でない図も、どんな集合を表しているのかを、数学的な記号で書けるようにしておきましょう。
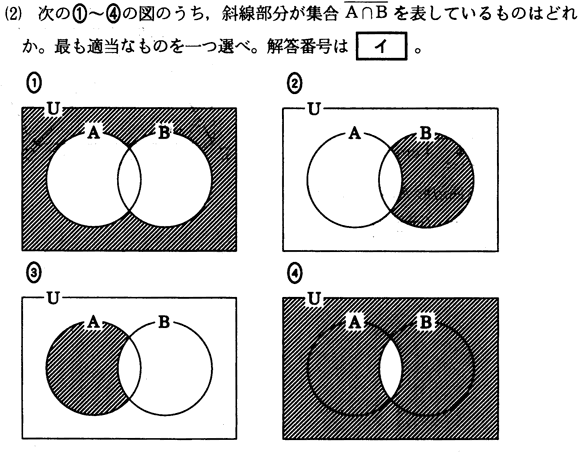
●解答・解説
1の白い部分はA∪Bです。それ以外の部分(A∪Bでない部分)なので、を表しています。また、上の本文で説明してありますが、∩も表しています。
2は、A以外の部分()のうち、Bと重なっている部分(共通部分)です。つまり、∩Bを表しています。
3は、B以外の部分()のうち、Aと重なっている部分(共通部分)です。つまり、A∩を表しています。
4の白い部分はA∩Bです。それ以外の部分(A∩Bでない部分)なので、を表しています。これが正解です。
高認の過去問にチャレンジ・2
次の問題は、問われ方が上の問題と少々違います。しっかり読めば解ける問題なので、惑わされずに頑張ってみましょう。また、それぞれの図は、どのような集合を表しているのか、数学的な記号で書けるようにしておきましょう。
20以下の自然数の集合を全体集合Uとし、その部分集合で、3の倍数全体の集合をA、4の倍数全体の集合をBとする。次の図の斜線部のうち、3の倍数であるが、4の倍数でない数の全体の集合を表しているものはどれか。
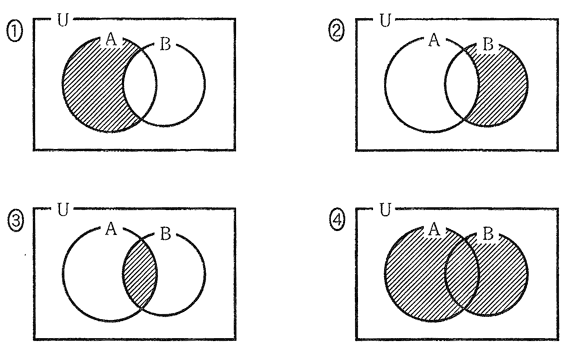
●解答・解説
ごちゃごちゃと書かれていますが、
A(3の倍数全体の集合)であり、B(4の倍数全体の集合)でないということなので、
Aの中でBでない部分ということになります。この時点で、1が正解であることがわかる方もいらっしゃると思います。
※この問題では、「○の倍数」などと表現して、難しそうに見えますが、この問題では気にしなくても正解できます。
言い換えると、Aとの共通部分ということです。つまりA∩です。A∩を表す図は1です。
ちなみに、2は∩Bです。
3は、A∩Bです。
4は、A∪Bです。
高卒認定スーパー実戦過去問題集 - 数学

数学は出題パターンが決まっており、毎回類似問題が出題されます。数学は特に過去問での勉強が効果的です。
高卒認定試験の過去問題6回分を掲載・解説。市販されている問題集の中で最も多くの過去問が掲載されています。しかも11月実施分の問題まで収録されている過去問題集は他にありません。
解答解説は、基本事項にも触れながら丁寧に説明されているので、苦手科目の克服にも最適。価格は少々高めですが、自信をもっておすすめできる過去問題集です。

