データの分析（代表値）

データ分析の問題

平成26年度の高卒認定／高認から、数学は学習指導要領に基づいた出題範囲となり、新たに「データの分析」が範囲に加わりました。本試験の出題を見ると、基礎的な内容がほとんどで、他の分野と比べて得点しやすい問題内容となっています。しかも配点は20点もあります。数学が苦手な人はこの分野を徹底的に勉強すれば、合格にグーッと近づくことができる、いわば「お得な分野」です。

まずは、用語を確認しよう！

データの分析では、いくつかの用語（中央値、最大値、範囲など）が登場します。これらの用語のほとんどは日本語として、そのまま理解すればよく、特に難しいことはありません。

データ分析の問題（特に、最大値、最小値、中央値などが問われる問題）では、まず、データを小さい順に並べることが基本です。問題のデータを小さい順に並べると、

1. 中央値はデータを小さい順に並べたときの真ん中のデータなので「7」となります。

※中央値は「メジアン」と呼ばれることもあります。

2. 最大値はデータの中で、一番大きなデータなので「10」となります。
3. 最小値はデータの中で、一番小さなデータなので「4」となります。
4. 範囲はデータの範囲。つまり「最大値と最小値の差」なので、10-4で「6」となります。
5. 平均値は、データの合計（=35）をデータの数(=5)で割ったものです。35÷5で「7」となります。

〔正解〕（1）7　（2）10　（3）4　（4）6　（5）7

いくつかの用語が出てきましたが、基本的には用語を日本語として、そのまま理解すればOKです。ただし、「中央値」については、少々注意が必要です。上の問題では、データの個数が5個（奇数）だったので、ズバリ真ん中のデータがありました。しかし、データの個数が6個のときなどは、前後のデータの真ん中の値（平均）が中央値です。例えば、

の場合は、7と8の真ん中が中央値、つまり、7.5が中央値になります（7+8）÷2 。

実戦問題にチャレンジ・1

次の問題は高卒認定／高認本試験で出題された問題です。選択肢を見ると「最小値」「中央値」などが登場するので、まずはデータを小さい順に並べます。頭の中で考えずに、必ず紙に書いて解いてみてください。

※スマホの方は横にすると見やすくなると思います。

　

━━ 解説 ━━
まずは、上のデータを小さい順に書き並べます。単純なミスを防止するため、書き並べた後は、データ数が10個であることも確認しましょう。また、問題文に「誤っているもの」とあることに注意してください。

　

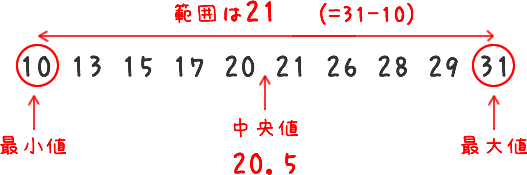
1. 「最小値」は10（正しい）ので、選択肢①は×
2. 「平均値」は、合計を計算してデータ数の10で割ります。合計は210なので、平均値は210÷10＝21（正しい）ので、選択肢②は×

※合計を計算するときは、端から順に計算するのではなく、一の位に着目して、合計が10になるものを組み合わせると効率的です。この問題では、「13と17」、「29と31」、「10と20」と組み合わせて計算すると楽です。計算済みのものは、2度計算しないように○などの印を付けておきましょう。

3. 「範囲」は、最大値と最小値の差なので、21です。これも正しいので、選択肢③は×
4. 「中央値」はデータを小さい順に並べたときの真ん中のデータ。ここでは、20と21の間になりますので、20.5です。よって、選択肢④は誤りなので、正解は④です。

最頻値とは

データ分析の問題では「最頻値」という用語も登場します。少し難しい用語ですが、これも日本語として、そのまま解釈すると「最も頻度の高い値」です。つまり、データの中で「最も多い値」です。次の問題を解いてみてください。

※「最頻値」は「モード」と呼ばれることもあります。

実戦問題にチャレンジ・2

　

━━ 解説 ━━
これは、最大値や最小値、中央値が問われている問題ではないので、並び変えなくても大丈夫です。

1. まず、「平均値」を求めます。合計を注意深く計算しましょう。合計は22になります。データの数は20（試合）なので、平均は22÷20を計算して、1.1となります。この時点で、選択肢①は×、選択肢②も×です。
2. 次に、最頻値ですが、最も多い値（データ）は１（11個）です。
3. 以上より、平均値は1.1、最頻値は1なので、④が正解です。