二次関数のグラフを選ぶ問題 高認・高卒認定対策
高卒認定（高認）試験の数学でよく出る「二次関数のグラフを選ぶ問題」の解説。頂点と向き（谷型、山型）がポイント。
二次関数のグラフを選ぶ問題は、二次関数を基本形に変形して、頂点の座標と山型か谷型かを見分ければOKです。ここでは高卒認定（高認）試験の数学の対策として基礎から丁寧に二次関数のグラフの選び方を解説します。
二次関数のグラフを選ぶ問題／高認対策
高卒認定試験で二次関数の「グラフを選ぶ問題」はよく出題されます。この問題の解き方のポイントは次の2つ (
と
) です。
2つめのポイントの式(基本形)は少々複雑ですが、これは今回の「グラフを選ぶ問題」だけでなく、さまざまな二次関数の問題を解くときの基本になりますので、頑張って覚えてしまいましょう。
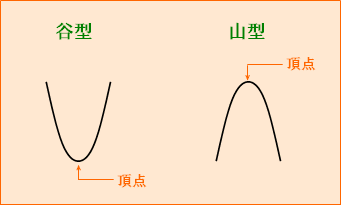
二次関数のグラフの形･･･谷型と山型の2つのタイプ
二次関数のグラフの形には「谷型」と「山型」の2つタイプがあることをまず覚えましょう。
二次関数の式の基本形
二次関数は、上記のように「グラフ」で表される場合もありますし、またあるときは「式」で表されることもあります。二次関数は、いわば「二面相」なのです。
二次関数の式を次のような基本形にすると、どんな形のグラフ（山型や谷型など）になるのかがわかります。
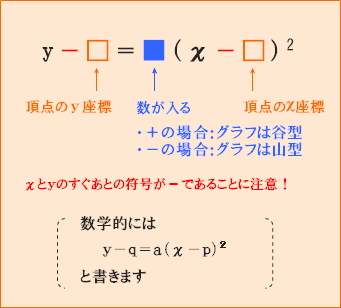
二次関数の式の基本形
二次関数の基本形をどのように見るのかを、このあと具体的に説明します。
谷型か山型の見分け方
二次関数の式が登場したら、まずすることは谷型か山型かを見分けることです。
二次関数が基本形になっていたら簡単に見分けられます。
上のポイントのとおり、
（ ）2の前の符号が＋だったら「谷型」、－だったら「山型」です。
例えば、
ｙ＝2（χ－2）2＋3 は「谷型」
ｙ＝－2（χ－2）2＋3 は「山型」
グラフの頂点の座標の求め方
グラフのイメージ
二次関数 ｙ＝2（χ－2）2＋3 を基本形にしてみましょう。
右辺の3を移行して、
ｙ－3＝2（χ－2）2
これが基本形です。これを見るとグラフの頂点の座標がわかるのです。
先のポイントと見比べると、
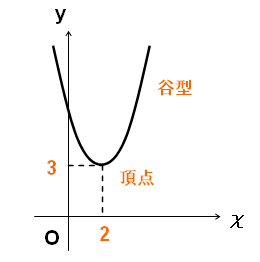
頂点の座標は（2，3）であることがわかります。
グラフのイメージは図の通りです。
二次関数のグラフを選ぶ問題では、（ ）2の前の数の符号（＋または－）から山型か谷型を判別。そして、式の基本形を見て頂点を求める。
それだけでOKなんです。
本試験ではニ次関数の式がいろいろな形で登場するので、まずは基本形に直します。基本形にすることができれば、あとは簡単です。
二次関数のグラフの概形／練習
では、少し練習してみましょう。必ず紙に書いて練習してください。
次の二次関数をグラフにしたときの形（谷型または山型）と頂点の座標を求めてみましょう。
（１） ｙ＝2（χ＋2）2＋5
まず、（ ）2の前の数の符号が＋2だから、グラフの形は「谷型」。
基本形はｙ－5＝2（χ＋2）2なので、 頂点の座標は（－2，5）
※頂点の符号（＋、－）でつまずいた人は、最初に説明した基本形をよく見直してみてください。それでも分からない場合は、頂点の座標はχとｙのすぐあとの数の符号が逆になったものと覚えましょう。
（２） ｙ＝（χ－3）2－2
（ ）2の前の数の符号が＋1（式では＋1は省略）だから、グラフの形は「谷型」。
基本形はｙ＋2＝（χ－3）2なので、 頂点の座標は（3，－2）
（３） ｙ＝－2（χ－1）2＋2
（ ）2の前の数の符号が－2だから、グラフの形は山型。
基本形はｙ－2＝－2（χ－1）2 なので頂点は（1，2）
（４）ｙ＝－3（χ－2）2
グラフの形は山型。
基本形は ｙ－0＝－3（χ－2）2と考えて 頂点は（2，0）
（５）ｙ＝χ2－2
グラフは谷型。
基本形は ｙ＋2＝（χ－0）2 と考えて 頂点は（0，－2）
（６） ｙ＝－3χ2
グラフの形は山型。
基本形は ｙ－0＝－3（χ－0）2 と考えて頂点は（0，0） つまり原点。
（７） ｙ＝χ2
グラフの形は谷型。
基本形は ｙ－0＝（χ－0）2 と考えて頂点は（0，0） これも原点。
高認過去問チャレンジ！
以上が理解できれば二次関数の「グラフを選ぶ問題」は、ほぼ完璧でしょう。 最後に高認の本試験で出題された問題にチャレンジしてみましょう。
最も適当なものはどれか。
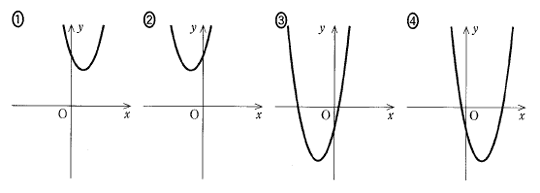
グラフの形は谷型。
基本形になおすと、ｙ＋３＝2（χ－１）２だから 頂点は（１、－３）
頂点が（１、－３）なのは
のみ。正解はです。
同じパターンの問題は毎年第１回または第２回のどちらかに出題されています。このページの内容が理解できれば、必ず正解できるはずです。ぜひ過去問にチャレンジしてみてください。
高卒認定（高認）試験の数学では、半分以上が、ほぼ同じようなタイプの問題が繰り返し出題されています。数学が苦手な人でも、過去問で練習して、難しく考えずに、解き方を覚えてしまえば合格が可能です。ぜひ、頑張ってください。
高卒認定スーパー実戦過去問題集 - 数学
数学は出題パターンが決まっており、毎回類似問題が出題されます。数学は特に過去問での勉強が効果的です。
高卒認定試験の過去問題6回分を掲載・解説。市販されている問題集の中で最も多くの過去問が掲載されています。しかも11月実施分の問題まで収録されている過去問題集は他にありません。
解答解説は、基本事項にも触れながら丁寧に説明されているので、苦手科目の克服にも最適。価格は少々高めですが、自信をもっておすすめできる過去問題集です。
※当サイトのオリジナルショップからお申込みいただくと送料が無料になります。
