箱ひげ図

箱ひげ図とは

データの最小値、最大値、第１四分位数、第２四分位数（＝中央値）、第３四分位数の5つの値を、箱（長方形）と、ひげ（線）で表現した図です。

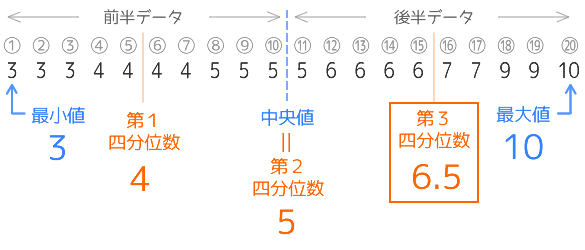
次のデータの箱ひげ図を書いてみます。

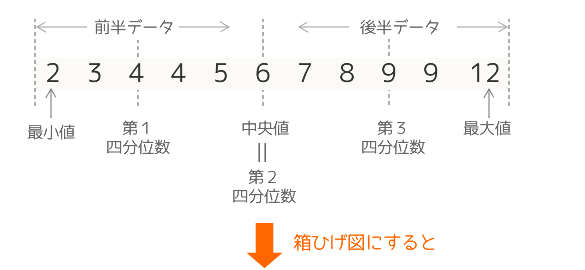
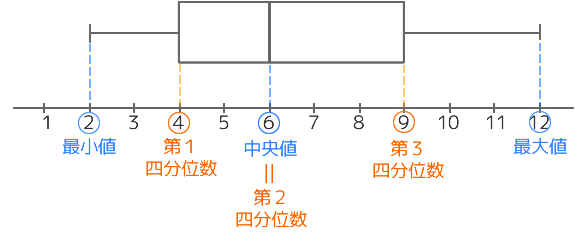
箱ひげ図の下の数直線の目盛は、元のデータを並べたものではなく、定規のように数を順に並べたもの（単純に1,2,3 …）です。そのため、もとのデータには同じ数（データ）が含まれることがありますが、箱ひげ図の数直線には、同じ数が含まれないことに注意してください。ここを曖昧にすると混乱しますので、特に注意してください。

※箱ひげ図に平均点を＋で記入する場合もあります。

※箱ひげ図はデータの分布（ばらつき）が表現され、複数のデータの分布を比較するときに用いられます。

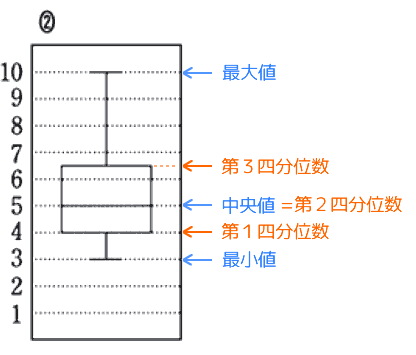
※箱ひげ図を縦に表示することもあります。その場合、下側が最小値、上側が最大値となります。

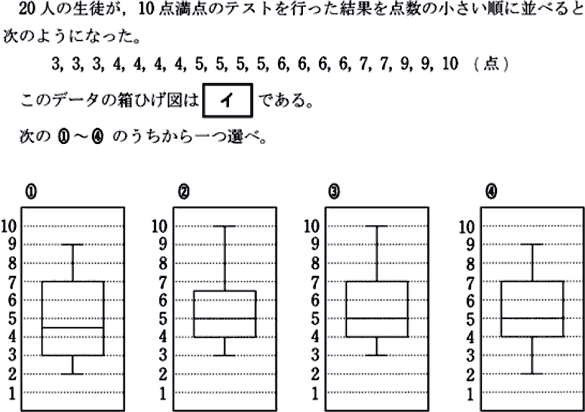
実戦問題にチャレンジ！

では、本試験問題にチャレンジしてみましょう。データが多く、少々手間がかかりますが、上の説明を理解していれば正解できます。また、箱ひげ図が縦型になっていることにも注意してください。

〔解説〕

1. データを見て、すぐわかるのは、最大値（＝10）と最小値（＝3）です。選択肢①と④は×です。
2. 残った選択肢②と③を見ると、中央値（＝5）と第１四分位数（＝4）は同じですが、第3四分位数が違っていますので調べます。

3. 20人の生徒のテスト結果なので、データ数は20個。前半データ10個と後半データ10個に分けて、その境界が中央値です。つまり、中央値は10番目のデータ（＝5）と11番目のデータ（＝5）の間になるので、中央値は5であることが確認できます。
4. 第3四分位数は、後半のデータ10個の真ん中（中央値）です。後半の真中は15番めのデータ（＝6）と16番目のデータ（＝7）の間にあります。よって、第3四分位数は、6.5となります。

5. 以上より、選択肢②が正解です。

高卒認定スーパー実戦過去問題集 - 数学

数学は出題パターンが決まっており、毎回類似問題が出題されます。数学は特に過去問での勉強が効果的です。

高卒認定試験の過去問題6回分を掲載・解説。市販されている問題集の中で最も多くの過去問が掲載されています。しかも11月実施分の問題まで収録されている過去問題集は他にありません。
解答解説は、基本事項にも触れながら丁寧に説明されているので、苦手科目の克服にも最適。価格は少々高めですが、自信をもっておすすめできる過去問題集です。

• 詳細はこちら

高卒認定スーパー実戦過去問題集

kino

※当サイトのオリジナルショップからお申込みいただくと送料が無料になります。