一次不等式の文章題(図式化して解く)
高卒認定試験の数学の文章題は、不等式の問題として出題されています。文章題といえば、数学が苦手な人ほど、敬遠してしまいがちです。でも、高認で出題される問題は基本問題です。日本語さえ理解できれば、日常の感覚で解ける問題がほとんです。
解法のポイントは、問題文の日本語を読取り図式化する(「うちわけ図」を書く)ことです。これだけで答えが出てしまう問題も少なくありません。図式化するときは、答えとして何を出すのか(目標)を常に意識することが大切です。
正解をゲットする秘訣は「問題文の日本語を正しく読み取り、それを図式化すること。」です。ここでは、過去問題を中心に、特に数学が苦手な人向けに解説します。
一次不等式の問題は「うちわけ図」で解決
例題1
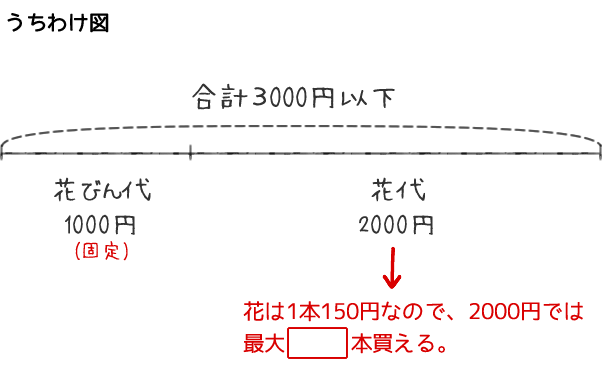
1000円の花びん1個と1本150円の花を何本か買って、代金の合計を3000円以下にしたい。このとき、花は最大【アイ】本まで買うことができる。
問題文から目標を読み取ります。「花の本数」です。この問題では「花の本数を求める」ということを答えが出るまで、ずっと意識します。次に問題文の日本語を図式化してみます。図に書いただけでも、答えがわかる人もいると思います。
↑この図で答えがわかったという人は、以下の説明文は不要です。例題2に進んでOKです。
- 3000円持っていて、花びんは1000円なので、花の代金として使えるのは2000円です。
- 花は1本150円なので、2000円で買える花の本数は、2000÷150で計算できます。
2000÷150=13.33333… - この13.33333…を勘違いしないように気をつけましょう。
計算では、2000円で買える花の本数は、13.33333…本です。
(13.33333…は、13 + 0.33333…です)
(0.33333…は3分の1。13本と3分の1本が買えます)
しかし、問題文を見ると【アイ】本となっているので、自然数で答えます。
自然数で考えると、13本は買えるけど、14本は買えない。
ゆえに、花は最大13本まで買うことができます。
例題2
山間部のある家庭では、冬季(11月~3月)に「暖房」、「給湯」、「その他」に使用するための灯油を購入している。今年の11月は、購入した灯油から「暖房」用として18L使用し、残りを半分ずつ「給湯」用と「その他」用に使用したい。「給湯」用の灯油を30L以上にしたいとき、購入する灯油は最低【アイ】Lである。
問題文(日本語)としては、少々複雑に見えますが、図式的に整理すると理解しやすいと思います。目標は購入する灯油の量です。「うちわけ図」を描きながら、問題文の情報を書き込みます。
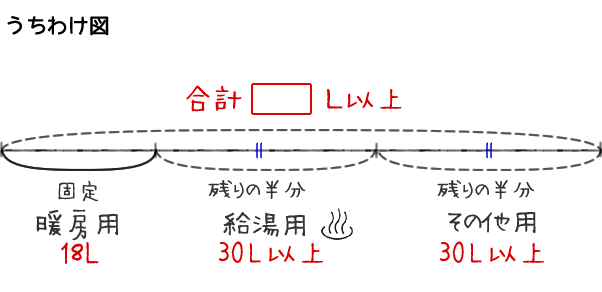
- 「暖房」用として18L使用し、残りを半分ずつ「給湯」用と「その他」用に使用するので、「給湯」用で30L以上使用するなら、「その他」用としても30L以上使用することになります。
- 「暖房」用として18L、「給湯」用と「その他」用の最低の使用量をそれぞれ30Lとして、合計すると、
18+30+30=78L
となり、これが購入する灯油の最低量です。
一次不等式の実戦問題にチャレンジ
高卒認定の過去問です。ぜひ、鉛筆を持って、「うちわけ図」を紙に書いて、自力で解いてみてください。
問題1
Aさんは、1ヵ月の基本使用料が2000円で、1分毎の通話料が25円かかる携帯電話を使っている。1ヵ月の基本使用料と通話料の合計を5000円以下にしたい。このとき、Aさんは最大【アイウ】分間通話することができる。
目標は「通話できる最大の時間(分)」です。問題文を読みながら「うちわけ図」を書いてみます。
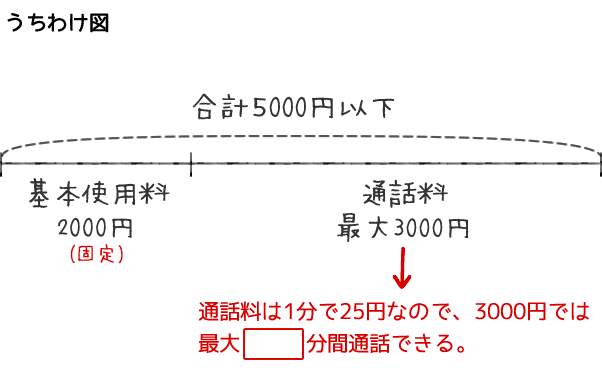
- 基本使用料と通話料の合計が5000円で、基本使用料が2000円なので、通話料は3000円使えます。
- 通話料は1分毎に25円なので、3000円で通話できる時間は、3000÷25で計算できます。
3000÷25=120 - ゆえに、最大120分間通話することができます。
問題2
1回に600kgの重さまで運ぶことができるエレベータに、体重80kgの人が乗って、1個30kgの荷物を何個か運ぶ。このとき、荷物は1回に最大【アイ】個まで運ぶことができる。
目標は「運ぶことのできる荷物の個数」です。問題文を読みながら「うちわけ図」を書いてみます。
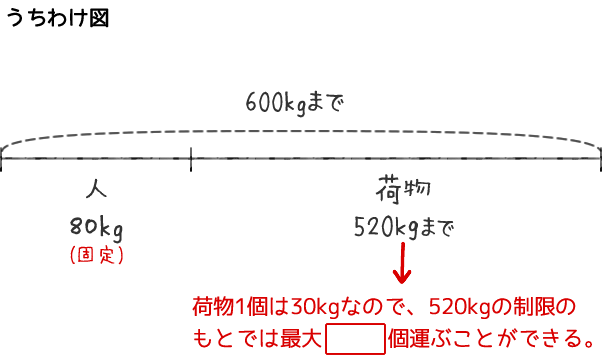
- 1回に600kgの重さまで運ぶことができるエレベータに、体重80kgの人が乗るので、荷物は最大520kgまで乗せることができます。
- 荷物は1個に30kgなので、520kgの制限のもとでは運ぶことのできる荷物の個数は、520÷30で計算できます。
520÷30=17.33333… - 計算結果が小数になってしまいましたが、例題1と同じように考えると、荷物は最大17個まで運ぶことができます。
問題3
3000円の予算で、1個150円のお菓子を何個か買って1つの箱に詰めて友人に送りたい。箱代が100円、送料が700円かかる時、お菓子は何個まで詰めることができるか。
一次不等式の解法のポイント
上記の問題は、高校の教科書では「一次不等式の利用」に相当する部分ですが、不等式を使わなくても感覚的に解けると思います。日常生活の中で数学的な考え方ができるかどうかが問われている問題だからです。ここで取り上げたような基礎レベルの問題では、上記のように図式化して、イメージを持って考えた方が数学的なセンスが養なわれますし、多少問われ方が違っても、対応できるようになるはずです。ただし、複雑な問題は不等式を立てて機械的に解いた方が、効率的です。次回は、少しレベルアップして、「図式化+不等式」で解く問題を紹介します。
高卒認定スーパー実戦過去問題集 - 数学

数学は出題パターンが決まっており、毎回類似問題が出題されます。数学は特に過去問での勉強が効果的です。
高卒認定試験の過去問題6回分を掲載・解説。市販されている問題集の中で最も多くの過去問が掲載されています。しかも11月実施分の問題まで収録されている過去問題集は他にありません。
解答解説は、基本事項にも触れながら丁寧に説明されているので、苦手科目の克服にも最適。価格は少々高めですが、自信をもっておすすめできる過去問題集です。

